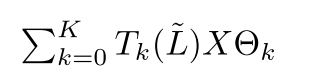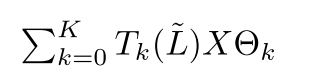论文地址：1606.09375

踩坑

  • 参数的初始化 开始的时候我使用的参数初始化方式为nn.init.normal_(self.kernels)，结果测试集精确度一直保持在0.4左右，改为pytorch默认的初始化方法精确度提高到了0.77左右。

加载数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import numpy as np
import scipy.sparse as sp
import torch

def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """Convert a scipy sparse matrix to a torch sparse tensor."""
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse_coo_tensor(indices, values, shape)

def load_cora(adj_path, node_path):
    nodes = np.genfromtxt(node_path, dtype=str)
    # 节点特征向量
    features = sp.csr_matrix(nodes[:,1:-1], dtype=np.float64)
    # 节点编号
    idx = np.array(nodes[:,0], dtype=np.int32)
    idx_map = {j:i for i,j in enumerate(idx)}
    # 标签
    labels = nodes[:,-1]
    classes = set(list(labels))
    classes_map = {c:i for i,c in enumerate(classes)}
    labels = np.array(list(map(classes_map.get, labels)))

    edges = np.genfromtxt(adj_path, dtype=np.int32)
    # 将论文索引与顶点编号对应，然后使用稀疏矩阵
    adj = np.array(list(map(idx_map.get, edges.flatten()))).reshape(edges.shape)
    # 此时构造的矩阵是一个上三角矩阵，因为论文编号小的论文是不会引用比它编号大的论文
    coo_adj = sp.coo_matrix((np.ones(adj.shape[0]), (adj[:,0], adj[:,1])), 
                         shape=(idx.shape[0], idx.shape[0]), dtype=np.int32)
    # 对称邻接矩阵
    A = coo_adj+coo_adj.T

    A, features = [sparse_mx_to_torch_sparse_tensor(e) for e in [A, features]]
    labels = torch.LongTensor(labels)

    return A, features, labels, idx_map, classes_map

ChebNet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class ChebConv(nn.Module):
    def __init__(self, in_channels, out_channels, k, normalize):
        super().__init__()
        self.normalize = normalize
        self.kernels = nn.Parameter(torch.FloatTensor(k+1, in_channels, out_channels))
        # self.reset_parameter()

    # def reset_parameter(self):
    #     nn.init.normal_(self.kernels)

    def forward(self, X, A):
        L = ChebConv.get_laplacian(A, self.normalize)
        # return L@X@self.kernels
        o = []
        for i,w in enumerate(self.kernels):
            o.append(self.chebyshev_polynomials(L,i)@X@w)
        return torch.stack(o, dim=0).sum(dim=0)

    def chebyshev_polynomials(self, L, k):
        if k == 0:
            return torch.eye(L.shape[0]).to(L.device)
        elif k == 1:
            return L
        else:
            return 2*L@self.chebyshev_polynomials(L,k-1)-self.chebyshev_polynomials(L,k-2)
    
    @staticmethod
    def get_laplacian(A, normalize):
        if normalize:
            # I = torch.eye(A.shape[0], dtype=A.dtype).to(A.device)
            # A = A + I
            D = torch.diag(torch.sum(A, dim=0)**(-1/2))
            L = -D@A@D
        else:
            D = torch.diag(A.sum(1))
            L = D - A
        return L
    
class ChebNet(nn.Module):
    def __init__(self, C, H, F, k, normalize, dropout_p):
        super().__init__()
        self.conv1 = ChebConv(C, H, k, normalize)
        self.conv2 = ChebConv(H, F, k, normalize)
        self.dropout = nn.Dropout(p=dropout_p)
    
    def forward(self, X, A):
        h = F.relu(self.conv1(X, A))
        if self.training:
            h = self.dropout(h)
        o = self.conv2(h, A)
        return o

Train

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def test_accuracy(net, X, Y, A):
    net.eval()
    outs = net(X, A).argmax(dim=1)
    train_outs, test_outs = outs[:140], outs[500:1500]
    train_labels, test_labels = Y[:140], Y[500:1500]
    train_score = train_outs[train_outs==train_labels].shape[0]/train_outs.shape[0]
    test_score = test_outs[test_outs==test_labels].shape[0]/test_outs.shape[0]
    return train_score, test_score

if __name__=='__main__':
    from utils import load_cora
    adj_path = 'Graph/data/Cora/cora.cites'
    node_path = 'Graph/data/Cora/cora.content'
    A, X, Y, idx_map, classes_map = load_cora(adj_path, node_path)

    device = torch.device('cuda')
    A, X, Y = [e.to(device) for e in [A.to_dense(), X, Y]]
    epochs, lr, weight_decay =200, 0.01, 5e-4

    net = ChebNet(X.shape[1], 32, len(classes_map), 2, True, 0.2).to(device)
    optimizer = torch.optim.Adam(net.parameters(), lr=lr, weight_decay=weight_decay)
    loss_fn = torch.nn.CrossEntropyLoss()

    loss_list = []
    t_total = time.time()
    for e in range(epochs):
        y_hat = net(X, A)
        optimizer.zero_grad()
        loss = loss_fn(y_hat[range(140)], Y[range(140)])
        loss.backward()
        optimizer.step()
        
        loss_list.append(loss.item())
        if e%10==0:
            print(f'epoch:{e}, loss:{loss.item()}')
    print("Total time elapsed: {:.4f}s".format(time.time() - t_total))
    print(test_accuracy(net, X, Y, A))
    plt.plot(loss_list)
    plt.show()

输出精度为(1.0, 0.767)