transformer结束后开始学习图神经网络了。
看了GCN的论文，下面从使用与模型背后的数学原理分别介绍。
处理的数据集是Cora数据集，即半监督学习的分类问题，最后精度和论文差不多。 # 直接使用 GCN的隐藏层传递公式如下：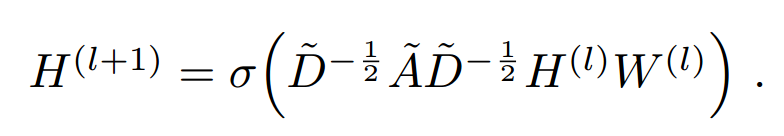
其中DAD这一堆东西是可以从图的结构（即邻接矩阵）直接给出的。\(H^0=X，X=(x_1,x_2,...,x_c),x_i是图的第i个节点的特征向量。W=(w_1,...,w_f)是需要拟合的参数，f代表通道数（channels）（和CNN的通道数相似），w_i是一个过滤器（filter）\) 层传递公式就是这样，下面用pyg实现：

import torch
import torch.nn.functional as F
from torch_geometric import nn
from torch_geometric.data import Data
from torch_geometric.datasets import Planetoid

class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, num_classify, dropout):
        super().__init__()
        self.conv1 = nn.GCNConv(in_channels, hidden_channels)
        self.conv2 = nn.GCNConv(hidden_channels, num_classify)
        self.dropout = torch.nn.Dropout(dropout)
    def forward(self, graph):
        x,edge_index = graph.x, graph.edge_index
        h = F.relu(self.conv1(x,edge_index))
        if self.training:
            h = self.dropout(h)
        o = self.conv2(h,edge_index)
        return o

def test_accuracy(net, cora_data):
    net.eval()
    out = net(cora_data)
    test_outs = out[cora_data.test_mask].argmax(dim=1)
    test_labels = cora_data.y[cora_data.test_mask]
    score = test_outs[test_outs==test_labels].shape[0]/test_outs.shape[0]
    return score

dataset = Planetoid(root='./data/Cora', name='Cora')
cora_data = dataset[0]
hidden_channels = 32
epochs, lr = 200, 0.01
weight_decay = 5e-4

net = GCN(cora_data.num_features, hidden_channels, dataset.num_classes, 0.2)
optimizer = torch.optim.Adam(net.parameters(), lr=lr, weight_decay=weight_decay)
loss_fn = torch.nn.CrossEntropyLoss()

device = torch.device('cuda')
net = net.to(device)
cora_data = cora_data.to(device)
for e in range(epochs):
    y_hat = net(cora_data)
    optimizer.zero_grad()
    loss = loss_fn(y_hat[cora_data.train_mask], cora_data.y[cora_data.train_mask])
    loss.backward()
    optimizer.step()

    print(f'epoch:{e}, loss:{loss.item()}')
print(test_accuracy(net, cora_data))

最后输入测试集准确率为0.812

从零实现GCN网络

import torch
from torch import nn
import torch.nn.functional as F
from scipy.sparse import csr_matrix, coo_matrix
import scipy.sparse as sp
import numpy as np
import matplotlib.pyplot as plt

adj_path = 'Graph/data/Cora/cora.cites'
node_path = 'Graph/data/Cora/cora.content'

def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """Convert a scipy sparse matrix to a torch sparse tensor."""
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse_coo_tensor(indices, values, shape)

def load_cora(adj_path, node_path):
    nodes = np.genfromtxt(node_path, dtype=str)
    # 节点特征向量
    features = csr_matrix(nodes[:,1:-1], dtype=np.float64)
    # 节点编号
    idx = np.array(nodes[:,0], dtype=np.int32)
    idx_map = {j:i for i,j in enumerate(idx)}
    # 标签
    labels = nodes[:,-1]
    classes = set(list(labels))
    classes_map = {c:i for i,c in enumerate(classes)}
    labels = np.array(list(map(classes_map.get, labels)))

    edges = np.genfromtxt(adj_path, dtype=np.int32)
    # 将论文索引与顶点编号对应，然后使用稀疏矩阵
    adj = np.array(list(map(idx_map.get, edges.flatten()))).reshape(edges.shape)
    # 此时构造的矩阵是一个上三角矩阵，因为论文编号小的论文是不会引用比它编号大的论文
    coo_adj = coo_matrix((np.ones(adj.shape[0]), (adj[:,0], adj[:,1])), 
                         shape=(idx.shape[0], idx.shape[0]), dtype=np.int32)
    coo_adj = coo_adj+coo_adj.T+sp.eye(coo_adj.shape[0])
    d = np.array(coo_adj.sum(1))
    d = sp.diags(np.power(d, -1/2).flatten())
    adj_hat = d@coo_adj@d

    # to tensor
    adj_hat = sparse_mx_to_torch_sparse_tensor(adj_hat)
    features = sparse_mx_to_torch_sparse_tensor(features)
    labels = torch.LongTensor(labels)

    return adj_hat, features, labels, idx_map, classes_map

class GCN(nn.Module):
    def __init__(self, in_channels, hidden_channels, num_classify, dropout, bias=False):
        super().__init__()
        self.conv1 = nn.Linear(in_channels, hidden_channels, bias=bias)
        self.conv2 = nn.Linear(hidden_channels, num_classify, bias=bias)
        self.dropout = nn.Dropout(dropout)
    def forward(self, x, adj):
        h = F.relu(adj@self.conv1(x))
        if self.training:
            h = self.dropout(h)
        o = adj@self.conv2(h)
        return o
    
def test_accuracy(net, x, adj, y):
    net.eval()
    out = net(x, adj)
    test_outs = out[140:1140].argmax(dim=1)
    score = test_outs[test_outs==y].shape[0]/test_outs.shape[0]
    return score


adj, X, Y, idx_map, classes_map = load_cora(adj_path, node_path)
hidden_channels = 32
epochs, lr = 200, 0.01
weight_decay = 5e-4

net = GCN(X.shape[1], hidden_channels, len(classes_map), 0.2)
optimizer = torch.optim.Adam(net.parameters(), lr=lr, weight_decay=weight_decay)
loss_fn = torch.nn.CrossEntropyLoss()

device = torch.device('cuda')
net = net.to(device)
adj, X, Y = [e.to(device) for e in [adj, X, Y]]

if __name__=='__main__':
    loss_list = []
    for e in range(epochs):
        y_hat = net(X, adj)
        optimizer.zero_grad()
        loss = loss_fn(y_hat[range(140)], Y[range(140)])
        loss.backward()
        optimizer.step()
        
        loss_list.append(loss.item())
        if e%10==0:
            print(f'epoch:{e}, loss:{loss.item()}')
    print(test_accuracy(net, X, adj, Y[140:1140]))
    plt.plot(loss_list)
    plt.show()