用seq2seq模型做机器翻译

Seq2Seq（Sequence to Sequence）用于处理序列到序列的任务。Seq2Seq 模型的核心思想是将一个序列转换成另一个序列。它由两个主要组件组成：编码器（Encoder）和解码器（Decoder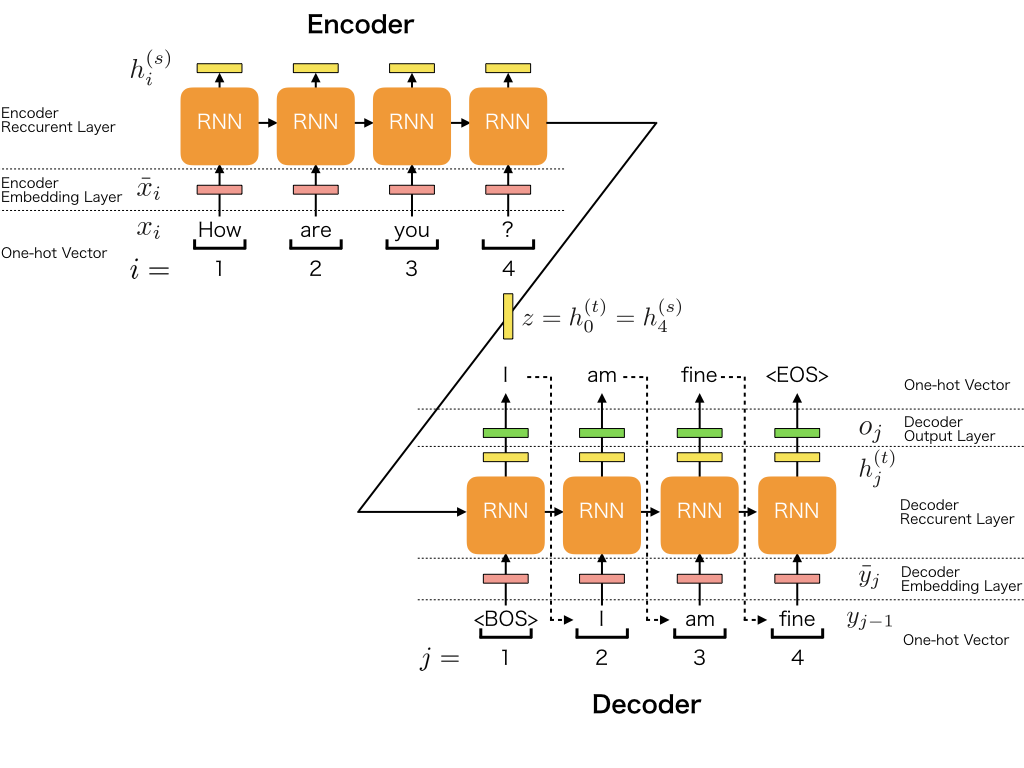）。 比如针对中文-英文机器翻译的问题，在训练时： - 中文序列作为编码器的输入，编码器最后一个时间点的隐藏层作为解码器的隐藏层的初始化。
- 使用教师强制（Teacher Forcing），即解码器生成输出序列时，真实的目标序列（教师提供的答案）被用作解码器的输入，而不是使用模型自身生成的先前符号。

在预测过程中，模型则根据先前生成的符号来预测下一个符号。这时，解码器的输入是模型自身生成的符号，而不再依赖于真实的目标序列。

seq2seq相当于是有两个接受不同输入的模型合并的模型。由于这里处理的是序列到序列的问题，所以在训练时有两个序列作为输入，分别输入编码器与解码器。编码器顾名思义是将中文序列给抽象成一个张量数据，然后将这个张量输入给解码器。解码器拿到编码中文序列和英文序列后开始优化自身的参数。

而在做预测时，解码器的输入就只有bos（开始）符号,在持续生成到eos（结束）符号时停止。

模型评估标准

BLEU（Bilingual Evaluation Understudy）是一种用于评估机器生成文本质量的指标，特别是在机器翻译的背景下。用于评估机器生成的翻译与一个或多个参考翻译之间的相似性。

BLEU分数的范围是0到1，其中1表示机器生成文本与参考翻译完全匹配。较高的BLEU分数通常表示更好的性能，但需要注意的是，BLEU有其局限性，不总是与人类对翻译质量的判断完全一致。它不能捕捉流畅度、语法或语义含义等方面，有时可能偏向过于字面的翻译。

n-gram表示文本中连续的n个项。其中，n是使用的n-gram级别。通常情况下，BLEU计算中使用1-gram到4-gram。 \[BLEU=exp(min(0,1-\frac{len_{label}}{len_{pred}}))\prod_{n=1}^k{p_n^{1/2^n}}\]

  • \(p_n\)是预测中所有n-gram的精度。 \[p_n=\frac{预测序列中n-gram在标签序列中匹配的次数}{预测序列中n-gram的总数}\] 例如，标签序列为A B C D E F，预测序列为A B B C D中
  • \(p_1=4/5\)，即预测序列1-gram为A B B C D，A有匹配，第一个B有匹配，第二个B没有匹配，C有匹配，D有匹配。
  • \(p_2=3/4\)，即预测序列2-gram为AB BB BC CD，AB有匹配，BB没有匹配，BC有匹配，CD有匹配
  • \(p_3=1/3\)
  • \(p_4=0\)

展开来看BLEU： - \(exp(min(0,1-\frac{len_{label}}{len_{pred}}))\)当预测序列的长度小于标签序列的长度时：这个值为1，这里是为了惩罚过短的预测。 - \(\prod_{n=1}^k{p_n^{1/2^n}}\)一般k取4。当n=4时次数靠近于0，是为了长匹配有高权重。
这样一个惩罚过短的预测，一个给长匹配有高权重。

损失函数

使用带mask的CrossEntropyLoss，mask相当于在原始张量上盖上一层掩膜，从而屏蔽或选择一些特定元素。

代码实现

import 

1
2
3
4
5
import torch
from torch import nn
from d2l import torch as d2l
import pandas as pd
from torch.utils.data import DataLoader
模型定义与损失函数 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class EncoderDecoder(nn.Module):
    def __init__(self, encoder, decoder) -> None:
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder

        self.enc_state = None
        self.dec_state = None
    def forward(self, X, X_valid_len, Y, Y_valid_len):
        enc_output, enc_state = self.encoder(X, X_valid_len)
        dec_output, dec_state = self.decoder(Y, enc_state, Y_valid_len)

        self.enc_state = enc_state
        self.dec_state = dec_state
        return dec_output

class Seq2seqEncoder(nn.Module):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers) -> None:
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size, num_hiddens, num_layers)

    def forward(self, x: torch.Tensor, *args):
        x = self.embedding(x)
        x = x.permute(1,0,2)
        # seq2seq的encoder的state是不需要保持之前的结构
        output, state = self.rnn(x)
        return output, state
    
class Seq2seqDecoder(nn.Module):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers) -> None:
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size+num_hiddens, num_hiddens, num_layers)
        self.linear = nn.Linear(num_hiddens, vocab_size)
    
    def forward(self, x:torch.Tensor, state:torch.Tensor, *args):
        # input x shape (batch_size, num_steps, embed_size)
        # input state shape (num_layers, batch_size, num_hiddens), only need last layer.so (batch_size, num_hiddens)
        x = self.embedding(x).permute(1,0,2) # x shape (num_steps, batch_size, vocab_size)
        context = state[-1].repeat(x.shape[0],1,1) # context shape (num_steps, batch_size, num_hiddens)
        x = torch.cat((x,context), dim=2)

        output, state = self.rnn(x, state)
        output = self.linear(output).permute(1,0,2)
        return output, state
    
def sequence_mask(X, valid_len, value=0):
    # X shape: batch_size * sequence_size
    batch_size, maxlen = X.size(0), X.size(1)
    mask = torch.arange((maxlen), dtype=torch.float32, device=X.device).repeat(batch_size, 1)
    valid_len = valid_len.reshape(-1, 1)
    mask = mask < valid_len
    X[~mask] = value
    return X

class MaskedSoftmaxCELoss(nn.CrossEntropyLoss):
    def forward(self, pred, label, valid_len):
        weights = torch.ones_like(label)
        weights = sequence_mask(weights, valid_len)
        self.reduction='none'
        unweighted_loss = super(MaskedSoftmaxCELoss, self).forward(pred.permute(0, 2, 1), label)
        weighted_loss = (unweighted_loss * weights).mean(dim=1)
        return weighted_loss
数据集加载 数据集使用chinese2english，中文使用字符one-hot，英文使用单词one-hot。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def tokens(path):
    eng = []
    chin = []
    with open(path, 'r', encoding='utf-8') as f:
        txt = f.read()
    for i,line in enumerate(txt.split('\n')):
        line = line.split('\t')
        line[0] = ''.join([' '+word if word in set(',.!?') else word for word in line[0].lower()])
        line[0] = line[0].split(' ')
        line[1] = list(line[1].replace(' ', ''))
        eng.append(line[0])
        chin.append(line[1])
    return chin, eng

def vocab_fn(tokens):
    seqs = []
    for seq in tokens:
        seqs += seq
    return d2l.Vocab(seqs, min_freq=2, reserved_tokens=['<pad>', '<bos>', '<eos>'])

class Eng2chinSet(object):
    def __init__(self, chin_vocab, eng_vocab, chin2engs, seq_size) -> None:
        self.chin_vocab, self.eng_vocab, self.seq_size = chin_vocab, eng_vocab, seq_size
        self.data = pd.DataFrame(chin2engs).T
    def corp_seq(self, seq, seq_size, vocab):
        n = len(seq)
        if  n>= seq_size:
            return seq[:seq_size-1]+[vocab['<eos>']], seq_size
        else:
            pads = [vocab['<pad>'] for _ in range(seq_size-n-1)]
            return seq + [vocab['<eos>']] +pads, n+1
    def __getitem__(self, idx):
        chin_seq, eng_seq = self.data.iloc[idx, :]
        chin_seq, chin_valid_len= self.corp_seq(self.chin_vocab[chin_seq], self.seq_size[0], self.chin_vocab)
        eng_seq, eng_valid_len= self.corp_seq(self.eng_vocab[eng_seq], self.seq_size[1], self.eng_vocab)
        chin_seq, chin_valid_len, eng_seq, eng_valid_len = [torch.tensor(x) for x in [chin_seq, chin_valid_len, eng_seq, eng_valid_len]]
        return chin_seq, chin_valid_len, eng_seq, eng_valid_len
    def __len__(self):
        return self.data.shape[0]

train 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
path = '/kaggle/input/english2chinese-simple-dataset/eng-chi.txt'
chin, eng = tokens(path)
chin_vocab, eng_vocab = vocab_fn(chin), vocab_fn(eng)
dataset = Eng2chinSet(chin_vocab, eng_vocab, (chin, eng), (20,15))

epochs, lr = 100, 0.005
batch_size = 1280
train_iter = DataLoader(dataset, batch_size=batch_size, num_workers=4)

encoder = Seq2seqEncoder(len(dataset.chin_vocab), 128, 256, 2)
decoder = Seq2seqDecoder(len(dataset.eng_vocab), 128, 256, 2)
net = EncoderDecoder(encoder, decoder)
loss_fn = MaskedSoftmaxCELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=lr)


device = torch.device('cuda')
net = net.to(device)
for e in range(epochs):
    epoch_loss = []
    for i, batch in enumerate(train_iter):
        X, X_valid_len, Y, Y_valid_len = [x.to(device) for x in batch]
        bos = torch.tensor([dataset.eng_vocab['<bos>']] * Y.shape[0],device=device).reshape(-1, 1)
        dec_input = torch.cat([bos, Y[:, :-1]], 1)
        y_hat = net(X, X_valid_len, dec_input, Y_valid_len)
        optimizer.zero_grad()
        loss = loss_fn(y_hat, Y, Y_valid_len).sum()
        epoch_loss.append(loss.item() / batch_size)
        loss.backward()
        optimizer.step()
        if i%100 ==0:
            print(f'epoch:{e}\tbatch:{i}\tloss:{loss.item() / batch_size}')
    epoch_loss = torch.tensor(epoch_loss).mean()
    print('loss: ', epoch_loss.item())

torch.save(net, 'chin2eng_batchsize1280.pt')
predict 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def predict_seq2seq(net, chin_sentence, chin_vocab, eng_vocab, num_steps,device):
    chin_tokens = chin_vocab[list(chin_sentence.replace(' ', ''))]
    chin_tokens, chin_valid_len = dataset.corp_seq(chin_tokens, 20, chin_vocab)
    enc_X = torch.unsqueeze(torch.tensor(chin_tokens, dtype=torch.long, device=device), dim=0)
    _, dec_state = net.encoder(enc_X, chin_valid_len)
    dec_X = torch.unsqueeze(torch.tensor([eng_vocab['<bos>']], dtype=torch.long, device=device), dim=0)
    output_seq = []
    for _ in range(num_steps):
        Y, dec_state = net.decoder(dec_X, dec_state)
        dec_X = Y.argmax(dim=2)
        pred = dec_X.squeeze(dim=0).type(torch.int32).item()
        if pred == eng_vocab['<eos>']:
            break
        output_seq.append(pred)
    return ' '.join(eng_vocab.to_tokens(output_seq))
predict_seq2seq(net, '今天早上吃的什么？', dataset.chin_vocab, dataset.eng_vocab, 50, device)
# 输出：what happened this morning lunch .
可以看到其实翻译效果一般，原因可能是数据集太小和模型太小。

注意力机制的一个例子

考虑下面这个回归问题：给定的成对的“输入－输出”数据集\({(x_1,y_1),...,(x_n,y_n)}\)，如何学习f来预测任意新输入x的输出\(\hat y=f(x)\)？
在attention的算法中，将 - 新输入x看为query - 数据集中的输入\(x_1,x_2,...,x_n\)看为key - 数据集中的输出\(y_1,y_2,...,y_n\)看为value
然后分别对比x与\(x_1,x_2,...,x_n\)的相似度，得到注意力分数\(a_1(x,x_1),...,a_n(x,x_n)\)，从而得到\(f(x)=\sum_{i=1}^na_i(x,x_i)y_i\)
在这里使用Nadaraya-Watson核回归来计算注意力分数。 \[a_i(x,x_i)=\sum_{i=1}^n\frac{K(x-x_i)}{\sum_{j=1}^nK(x-x_j)}\] 其中K是核，在这里选择高斯核函数。 \[K(u) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{u^2}{2}\right)\] 综上 \[f(x)=\sum_{i=1}^nsoftmax(-\frac12(x-x_i)^2)y_i\] ## 实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用中文字体（例如宋体）
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

def f(x):
    return 2*torch.sin(x) + x**0.8
def net(input, x_train, y_train):
    scores = []
    output = []
    for x in input:
        score = torch.softmax(-0.5*(x-x_train)**2, dim=0)
        y_hat = torch.matmul(score, y_train)
        output.append(y_hat)
        scores.append(score)
    return torch.stack(output, dim=0), torch.stack(scores, dim=1)

x_train,_ = torch.sort(torch.rand(100)*10)
y_train = f(x_train)
y_hat, scores = net(x_train, x_train, y_train)
y_hat, y_train

plt.plot(x_train, y_train, label='真实值')
plt.plot(x_train, y_hat, label='预测值')
plt.legend()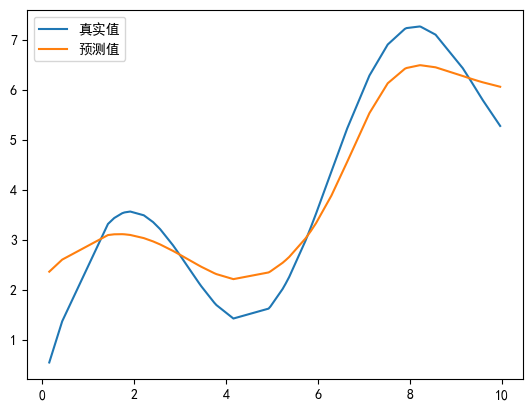
Alt text
1
2
3
plt.figure(figsize=(4,3))
heatmap = plt.imshow(scores, cmap='Reds')
plt.colorbar(heatmap)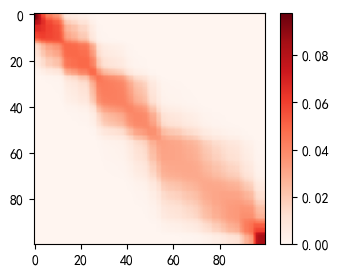
下图是注意力分数矩阵的热力图，图中(i,j)位置表示\(a_j(x_i,x_j)\)，可以看出序列X中每一个元素给周围元素的权重比较大。 Alt text

真正的注意力机制(Attention)

将query记为q，key记为k，value记为v。现在\(q\in R^q, k\in R^k, v\in R^v\)，k、v是成对出现\({(k_1,v_1),(k_2,v_2),...,(k_n,v_n)}\). 上面的例子中计算注意力分数的函数是一个提前设计好的函数,没有需要学习的参数.从效果上看拟合效果一般.下面引入新的计算注意力分数的算法:
1.Additive Attention:
\(a(q,k_i)=W_v^Ttanh(W_kk_i+W_qq)\)
其中\(W_k\in R^{h\times k}, W_q\in R^{h\times q}, W_v\in R^h\),故需要学习的参数为\(W_k,W_q,W_v\)
从设计上看Additive Attention就是三个Linear层做运算的结果.
2.Dot-Product Attention:
如果q与k的向量维度相同,那么可以
\(a(q,k_i)=\langle q,k_i\rangle/\sqrt d\)
是做内积来计算,d是向量q的维度,在这里也没有需要学习的参数.

self-attention设计思想

Self-attention（自注意力机制）是一种在深度学习模型中用于捕捉序列内部关系的重要机制。Self-attention主要用于处理序列数据，Self-attention的优势在于它能够捕捉序列中任意两个位置之间的关系，而不受到距离的限制。这使得模型能够更好地理解长序列的依赖关系。
Hung-yi Lee:【機器學習2021】自注意力機制 (Self-attention) (下)
对于一个输入序列\(X=(a^1, a^2, a^3, a^4)\),self-attention从序列本身抽取出query,key,value. \[ query=W^qX=W^q(a^1,a^2,a^3,a^4) \\\\ key=W^kX=W^k(a^1,a^2,a^3,a^4) \\\\ value=W^vX=W^v(a^1,a^2,a^3,a^4) \\\\ \] 再使用Dot-Product来计算注意力分数(attention scores).如下图所示: 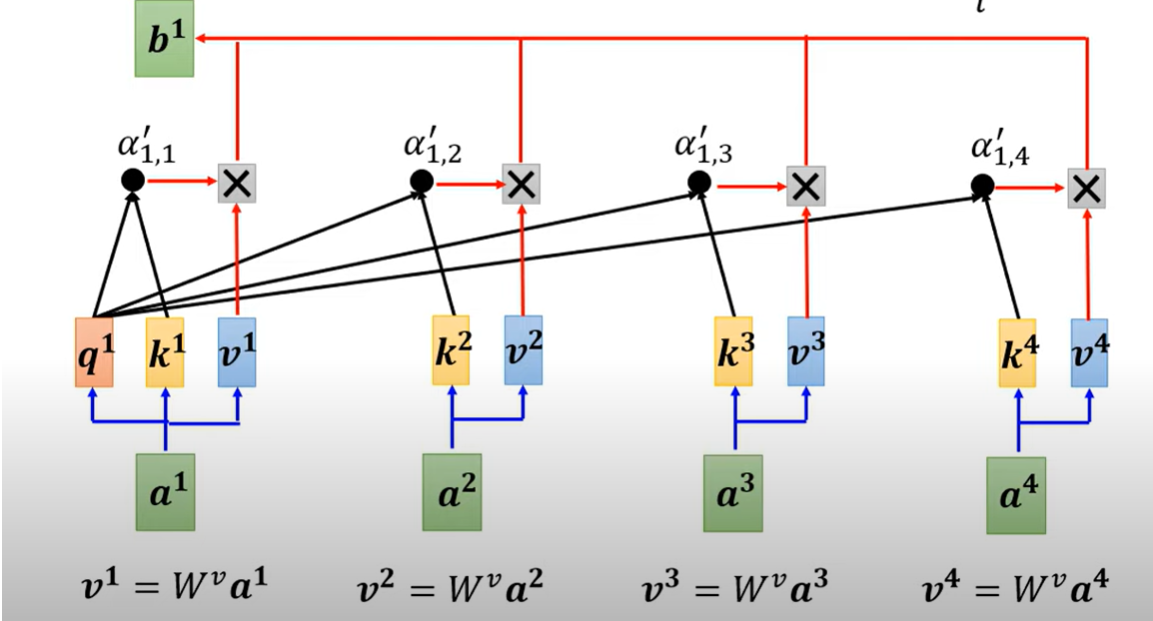- \((b^1, b^2, b^3, b^4)\)是self-attention层的输出。

从矩阵乘法看

\[ Q=W^qX=W^q(a^1,a^2,a^3,a^4) \\ K=W^kX=W^k(a^1,a^2,a^3,a^4) \\ V=W^vX=W^v(a^1,a^2,a^3,a^4) \\ \alpha_{11},\alpha_{12},\alpha_{13},\alpha_{14} = (q^1,k^1),(q^2,k^2),(q^3,k^3),(q^4,k^4)其中(,)表示向量内积 \\\\ 令A= \begin{bmatrix} \alpha_{11} & \alpha_{21} & \alpha_{31} & \alpha_{41} \\ \alpha_{12} & \alpha_{22} & \alpha_{32} & \alpha_{42} \\ \alpha_{13} & \alpha_{23} & \alpha_{33} & \alpha_{43} \\ \alpha_{14} & \alpha_{24} & \alpha_{34} & \alpha_{44} \\ \end{bmatrix} =K^TQ=(k^1,k^2,k^3,k^4)^T(q^1,q^2,q^3,q^4) \\ \hat{A} = Softmax(A/\sqrt d) \\ B = V\hat{A} = (v^1,v^2,v^3,v^4)\hat{A} \] 综上 \[B = V\sigma(K^TQ/\sqrt d)\] 其中\(\sigma\)是Softmax