问题：手写数字识别

识别图片所表示的数字。 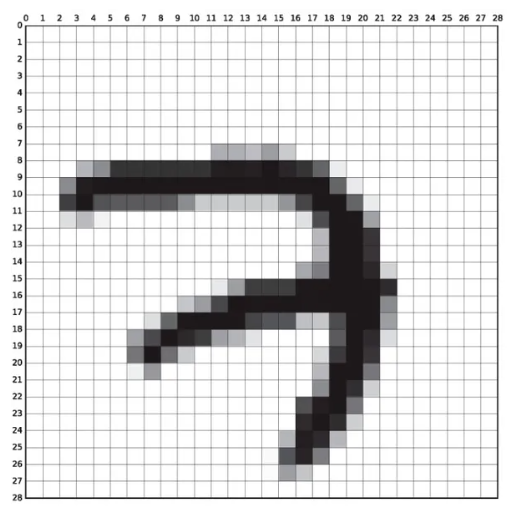## 数据集 MNIST数据集包含60000张训练图片和10000张测试图片，每张图片都有对应的标签，标签表示图片中的数字。训练集通常用于训练模型，而测试集用于评估模型的性能。
每张图片都是28x28像素的灰度图像，标签是0到9之间的数字，表示图片中的手写数字。即输入模型的数据是一个28x28的矩阵。

模型评估标准

准确率（Accuracy） 准确率，指的是正确预测的样本数占总预测样本数的比值，其公式如下： \[Accuracy=\frac{正确预测样本数}{总预测样本数}\]

多层感知机模型

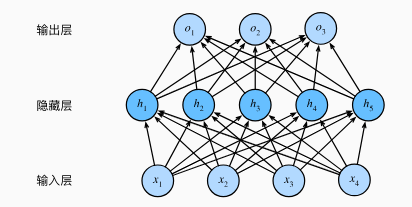它由一个输入层、一个或多个隐藏层和一个输出层组成，每个层都包含多个神经元（也称为节点或单元）。
下面看一个单隐藏层的多层感知机模型：
输入层为28*28=784维向量，用X表示输入的值
隐藏层为256维向量，用H表示隐藏层的值
输出层为10维向量，用O表示输出层的值，且O中数值最大的分量所对应的位置就是我们的最终预测类别

则 \[ H = \sigma(W_hX+b_h) \\ O = W_oH + b_o \] 其中\(\sigma\)是激活函数，为什么要使用激活函数？因为如果没有激活函数那么模型就变为了: \[O = W_o(W_hX+b_h) + b_o = (W_oW_h)X + (W_ob_h + b_o) = WX + b\] 就回到了一个线性模型。

激活函数

ReLU

\(ReLU(x) = max(0,x)\)
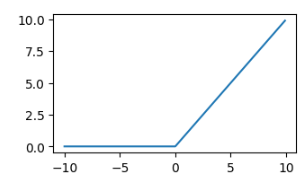各种各样的激活函数可以引入非线性变换，使得模型能够学习更复杂的模式。

总结

模型定义为： \[ H = \sigma(W_hX+b_h) \\ O = W_oH + b_o \] 其中需要通过优化算法来拟合参数\(W_h,b_h,W_o,b_o\)， 显然Wh可以看作一个256x784的矩阵，bh是一个256维的向量，Wo是一个10x256的矩阵，bo是一个10维的向量。

损失函数

交叉熵损失函数（Cross-Entropy Loss）

多分类问题的损失函数通常用于衡量模型在将样本分配到多个类别中的准确程度。以下是一些常见的多分类问题的损失函数：

$ = -_{i=1}^{C} y_i(p_i) $
其中C是类别数，y是实际类别的one-hot编码，\(y_i\)就是y的第i维数值，p是模型的输出，\(p_i\)就是p的第i维数值 即在我们的问题中C=10，由于我们有10个类别，例如类别3的one-hot编码就是\([0,0,0,1,0,0,0,0,0,0]\)

优化算法

SGD

它是梯度下降的一种变体，SGD每次只使用一个样本（或一个小批量样本）来更新模型参数。

SGD（Stochastic Gradient Descent）的更新规则可以用以下的数学公式表示：

给定目标函数 $ J() $，其中 $ $ 表示模型的参数，SGD的参数更新规则如下：

$ _{t+1} = _t - J(_t; x^{(i)}, y^{(i)}) $

在这个公式中：

  • $ _{t+1} $ 是更新后的参数。
  • $ _t $ 是当前的参数。
  • $ $ 是学习率（learning rate），用于控制每次更新的步长。
  • $ J(_t; x^{(i)}, y^{(i)}) $ 是目标函数关于参数 $ _t $ 在样本 $ (x^{(i)}, y^{(i)}) $ 上的梯度。

$ (x^{(i)}, y^{(i)}) $ 表示从训练集中随机选择的一个样本。这就是“随机”（Stochastic）梯度下降的来源，因为每次迭代都只使用一个样本来进行参数更新。

训练模型

最后模型精确率为97.79

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import torch
from torch import nn
from torch.utils import data
from torchvision import datasets, transforms

batch_size = 64
epochs = 10
lr = 0.5

transform = transforms.Compose([transforms.Resize((28,28)) ,transforms.ToTensor()])
train_data = datasets.MNIST('./data/minst', train=True, transform=transform, download=True)
train_iter = data.DataLoader(train_data, batch_size=batch_size, num_workers=4)

class Net(nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super().__init__(*args, **kwargs)

        self.f = nn.Flatten()
        self.l = nn.Sequential(nn.Linear(28*28, 256), nn.ReLU(), nn.Linear(256, 10))
    
    def forward(self, x):
        x = self.f(x)
        x = x.reshape((-1,28*28))

        return self.l(x)

net = Net()
loss_fn = nn.CrossEntropyLoss()
updater = torch.optim.SGD(net.parameters(), lr=lr)


device = torch.device('cuda')
net = net.to(device)
for e in range(epochs):
    for x,y in train_iter:
        x,y = x.to(device), y.to(device)
        y_hat = net(x)
        loss = loss_fn(y_hat, y)
        updater.zero_grad()
        loss.backward()
        updater.step()
        
    print('loss: ', loss.item())


test_data = datasets.MNIST('./data/minst', train=False, transform=transform, download=True)
test_iter = data.DataLoader(test_data, batch_size=1, num_workers=4)

def accuracy(net, data_iter):
    count = 0
    all = 0
    for x,y in data_iter:
        x,y = x.to(device), y.to(device)
        y_hat = net(x)
        maxs, indexs = torch.max(y_hat, dim=1)
        if indexs==y: count+=1
        all += 1
    return all, count

accuracy(net, test_iter)
# 输出 (10000, 9779)