机器学习算法数据降维PCA

简介

@维基百科

在多元统计分析中，主成分分析（英语：Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。具体地，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化或预处理敏感（相对缩放）。

本文内容皆源自Andrew Ng

目的

1.实现数据压缩 2.实现数据在2D或3D中可视化

算法

PCA(主成分分析)

步骤

1.数据预处理

采用归一化方法，是的均值为0，方差为1。 步骤，1.均值为0 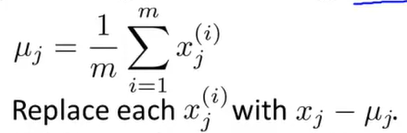2.方差为1 \(x_j^{(i)}=\frac{x_j-\mu}{s_j}\)s_{j}为标准差即为样本中第j维数据的标准差

2.协方差矩阵

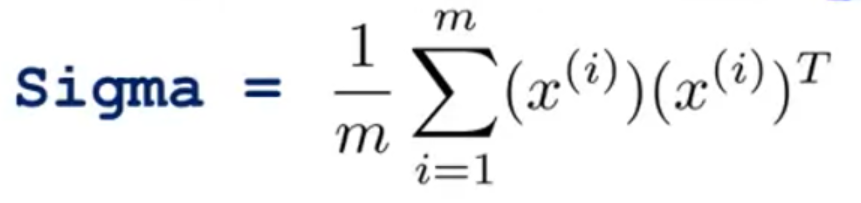
@维基百科 z即使PCA特征缩放后的结果。

3.选择适当的参数K

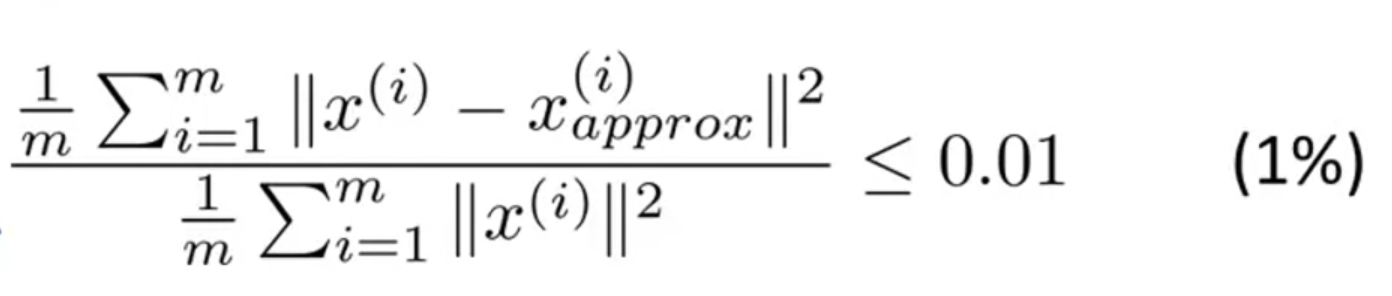其中\(x_apporx^{(i)}\)为\(x^{(i)}\)在压缩向量上的投影。 S：对角矩阵，对角元素是Sigma的奇异值，非负且按降序排列。

建议

一般在机器学习中，先判断PCA处理可以给你的学习带来什么，做决定。 一般先在原数据上做学习处理，若学习速度太慢，再考虑使用PCA。 一般防止过拟合不采用PCA，而是加上正则化项。