简介

1
2
3
4
5
在机器学习中，支持向量机（英语：support vector machine，常简称为SVM，又名支持向量网络[1]）是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。
给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。
SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。
然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。
@维基百科

之下的总结顺序皆来自Andrew Ng

我的理解

对于我个人的理解，这是一个尝试实现将新输入的数据分类的算法。 即预先准备标记点

\[ \begin{bmatrix} f_1\\ f_2\\ {\vdots}\\ f_n\\ \end{bmatrix} \]

对于一个新输入的数据\(x_1\)。 \(x_1\)经过核函数处理后，得到f矩阵

\[ \begin{bmatrix} f_1^1\\ f_2^1\\ {\vdots}\\ f_n^1\\ \end{bmatrix} \]

后带入相似度函数

\[ h_{\theta}=\theta_{0}+\theta_{1}*f_{1}+\theta_{2}*f_{2}+...+\theta_{n}*f_{n} \]

得到值后根据值是否大于0进行分类。 然后将训练集带入优化函数优化\(\theta\)。 注：需要说明的是核函数和相似度函数 核函数：常用的有线性核函数（即没有核函数）和高斯核函数（如下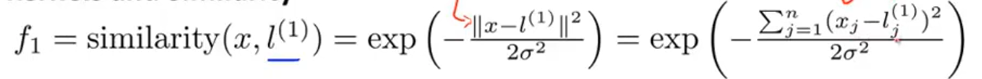） 高斯核函数 相似度函数：

\[ h_{\theta}=\theta_{0}+\theta_{1}*f_1+\theta_{2}*f_2+...+\theta_{n}*f_n \]

高斯核函数图像： 高斯核函数图像 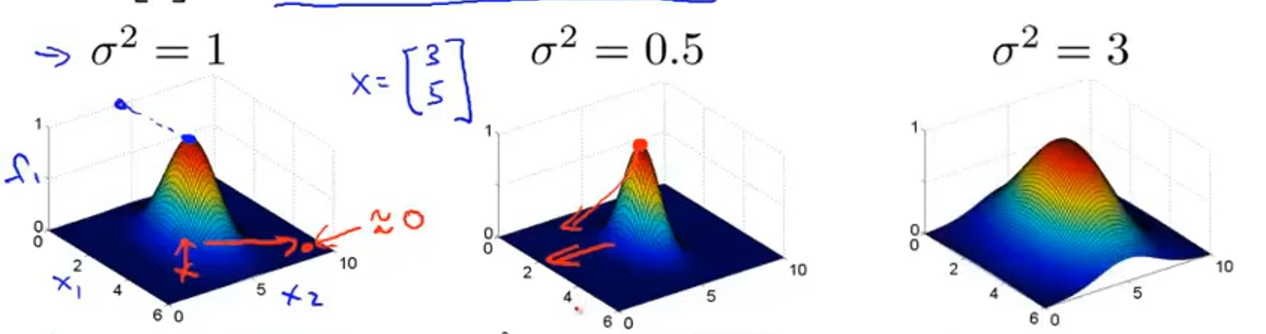# 优化目标 优化函数为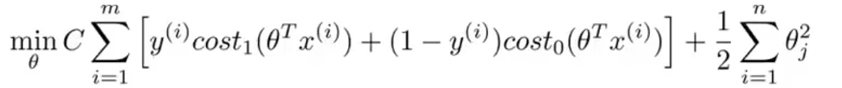： 优化函数

即对于支持向量机的核函数为线性核函数时，分类的决策边界为一条直线，例如： 决策边界

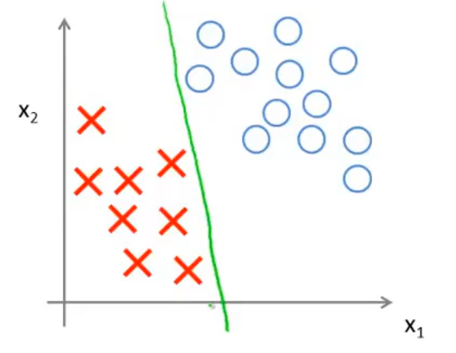
根据优化函数将线性决策边界化为如下黑线所示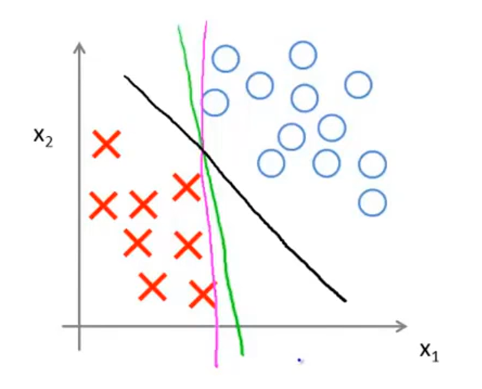： 决策边界

为什么这样优化？详见Andrew Ng的课程

使用高斯核函数

将输入\(x_1\)带入高斯核函数后计算出\(f_i=x_1^Tf_i\),然后将\(f_i\)组合成矩阵f。 判断\(\theta^Tf\)是否大于0，实现分类。

sklearn 实现SVM分类

参考

pluskid
wizardforcel
dongquanc
studyai scoring参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 数据集样本生成
from sklearn.datasets import make_blobs
from sklearn.datasets import make_circles

# model
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV

# 玩具数据集
from sklearn.datasets import load_iris

# train test split
from sklearn.model_selection import train_test_split

线性核SVM

1
2
3
%matplotlib notebook
x, y = make_blobs(n_samples=50, n_features=2, centers=2, cluster_std=2, random_state=10)
plt.scatter(x[:,0], x[:,1], marker="o", c=np.squeeze(y), s=30)
<IPython.core.display.Javascript object>

<matplotlib.collections.PathCollection at 0x2300092dd88>
1
2
3
4
5
6
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=10)

svc = SVC(C=1, kernel='linear')
svc.fit(x_train, y_train)
svc.score(x_test, y_test)
1.0
1
2
3
4
5
# w0
print(svc.intercept_)

# w1~wn
print(svc.coef_)
[1.04204619]
[[-0.08757647  0.31572354]]
1
2
3
4
5
6
7
8
9
10
11
12
fig = plt.figure()
ax = plt.axes(projection='3d')

xx = np.arange(-15, 10, 1)
yy = np.arange(-15, 10, 1)

X, Y = np.meshgrid(xx, yy)
Z = svc.intercept_[0] + svc.coef_[0,0] * X + svc.coef_[0,1] * Y
ax.plot_surface(X, Y, Z, cmap='rainbow')

z = svc.intercept_[0] + svc.coef_[0,0] * x[:,0] + svc.coef_[0,1] * x[:,1]
ax.scatter3D(x[:,0], x[:,1], z)
<IPython.core.display.Javascript object>

<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x23006f8b0c8>

高斯核SVM

1
2
3
x, y = make_circles(100, random_state=5)
ax2 = plt.axes()
ax2.scatter(x[:,0], x[:,1], marker="o", c=np.squeeze(y), s=30)
<IPython.core.display.Javascript object>

<matplotlib.collections.PathCollection at 0x23007444088>
1
2
3
4
5
6
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=10)

rbfSvc = SVC(C=1, kernel='rbf', gamma=2)
rbfSvc.fit(x_train, y_train)
rbfSvc.score(x_test, y_test)
1.0
1
2
3
# 若将此处的核函数切换为线性核
svc.fit(x_train, y_train)
svc.score(x_test, y_test)
0.4666666666666667

使用玩具数据集iris

1
2
3
4
iris = load_iris()

x_train, x_test, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.4, random_state=10)
1
2
3
rbfSvc = SVC(C=1, kernel='rbf', gamma=2)
rbfSvc.fit(x_train, y_train)
rbfSvc.score(x_test, y_test)
0.95
1
2
3
svc = SVC(C=1, kernel='linear')
svc.fit(x_train, y_train)
svc.score(x_test, y_test)
0.9666666666666667
1
2
3
4
5
6
7
# 使用网格搜索法
svc = SVC(C=1, kernel='linear')
param = {
    'C': [0.5, 1.0 ,1.5],
    'kernel': ['rbf', 'linear'],
    'gamma': [0.5, 1.0, 1.5, 2.0]
}
1
2
gv = GridSearchCV(estimator=svc, param_grid=param, cv=5)
gv.fit(iris.data, iris.target)
GridSearchCV(cv=5, error_score='raise-deprecating',
             estimator=SVC(C=1, cache_size=200, class_weight=None, coef0=0.0,
                           decision_function_shape='ovr', degree=3,
                           gamma='auto_deprecated', kernel='linear',
                           max_iter=-1, probability=False, random_state=None,
                           shrinking=True, tol=0.001, verbose=False),
             iid='warn', n_jobs=None,
             param_grid={'C': [0.5, 1.0, 1.5], 'gamma': [0.5, 1.0, 1.5, 2.0],
                         'kernel': ['rbf', 'linear']},
             pre_dispatch='2*n_jobs', refit=True, return_train_score=False,
             scoring=None, verbose=0)
1
2
print(gv.best_score_)
print(gv.best_params_)
0.9866666666666667
{'C': 0.5, 'gamma': 0.5, 'kernel': 'linear'}